https://www.youtube.com/watch?v=UNIF-jHY2Rk
들어가기 전에
https://heesleisure.tistory.com/55
[Econometrics, 계량경제학] 데이터 구조와 고정 효과(Fixed Effect)
https://www.youtube.com/watch?v=yZOTgQfVfxQ 데이터 구조Cross-sectional Data : 여러 유닛, 특정 시점의 정보를 포함 (서베이 등 데이터를 모음)Time-Series Data : 하나의 유닛, 시간에 따른 변화 (주식 가격, 국가의 G
heesleisure.tistory.com
이전 글을 먼저 읽어보시면 이해가 빠르실 겁니다!
How Fixed Effects Work for Causal Inference
어떤 방식으로 작동하는지 toy example로 살펴보자~
아래 패널 데이터(longitudinal)

Customer 1, 2: Treatment
Customer 3: Control
Gender, Age, Address는 영원불변하진 않겠지만 우리가 분석하는 기간 내에는 변하지 않으므로
time-invariant convariate로 간주
Time-invarant한 confounder는 Unit Fixed Effect로 고정된다
Fixed Effect는 Time-invariant한 variable을 다 흡수한다고 했잖아여
왜냐면? 이 고객을 나타내는 더미변수들이 time-invariant한 특성을 다 설명할 수 있기 때문이져
예를 들어봅시다. Gender는 d1, d2, d3로 100%로 나타낼 수 있잖아여.
Gender = 1*D1 + 0*D2 + 0*D3
Age = 20*D1 + 21*D2 + 22*D3
따로 변수가 없어도 더미변수로 표현할 수 있다는 것 → Perfectly collinear

기존의 Baseline이라고 할 수 있는 수치값도 Fixed Effect에 반영이 됩니다.
예를 들어, Customer 1의 첫날 구매량이 50이라면 이게 기준치가 된다.
그래서 Fixed Effect를 모형에 추가함으로써
다음날 구매량인 70 중 50이 baseline이며 fixed effect에 반영되고, 남은 20(변화량)만 분석에 활용하게 되는 것
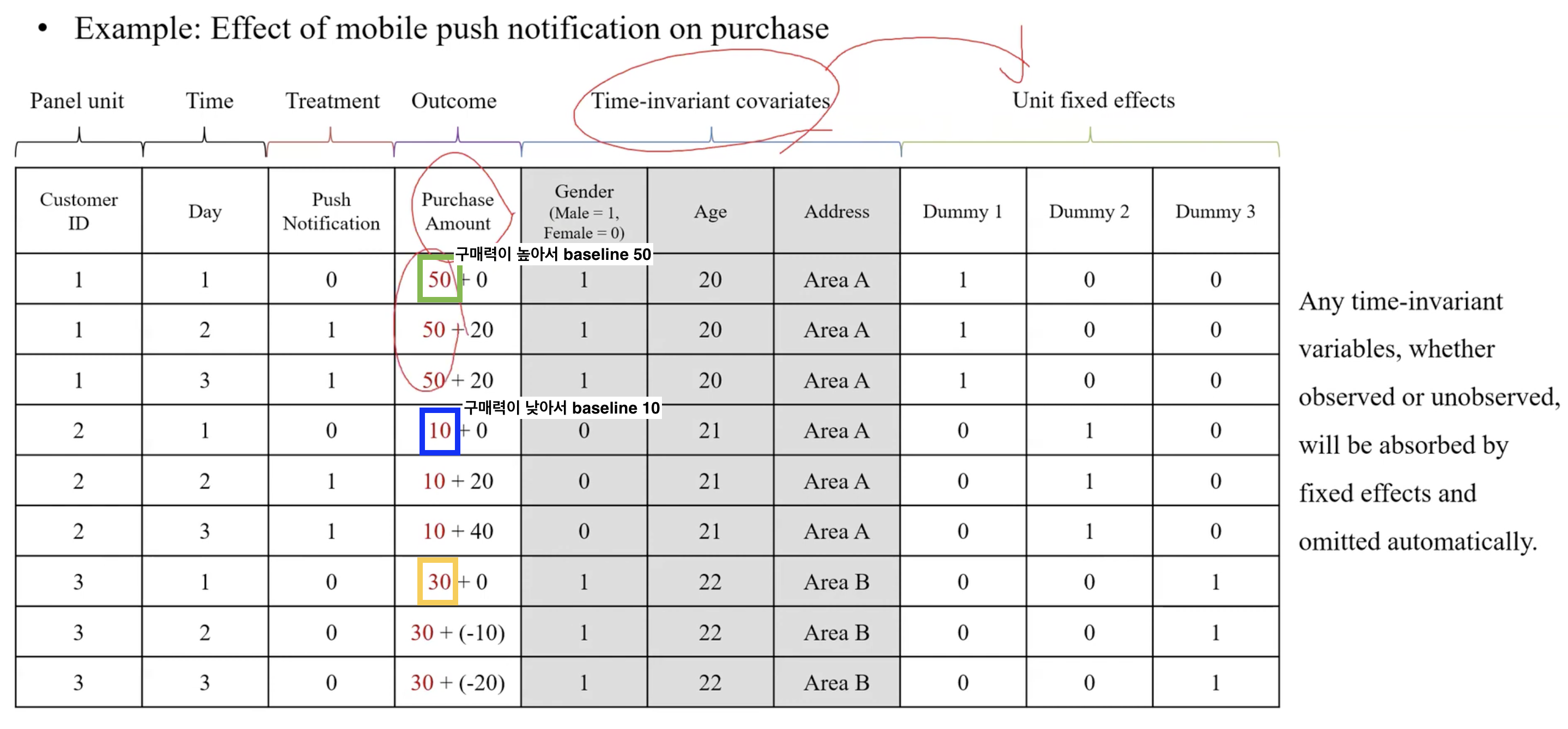
이해하기 쉽게 계산을 해봅시다
Q1: Fixed Effect롤 고려하지 않은 순수 계산, 그냥 Treatment 그룹과 Control 그룹의 변화량을 비교함
Q2: Unit Fixed Effect를 추가, 그룹 더미를 넣어줌으로써 '그룹 내' 비교가 가능해짐 (아래 그림 중 우측 참고)
고객 1과 고객 2의 변화량을 평균내서 대충 treatment가 발생하면 이 정도 변해요~ 하고 평균내서 말해주는 것
- 근데? 잘 보면 Control group은 계산에 넣어주지 않는다. 왜? treatment로 인한 변화가 아니니까. (Q3까지 이어짐)
- 즉, Control group이 아무런 영향을 끼치지 않는다.
Q4: 위에서 Unit Fixed Effect를 통해 Time-invariant Confounder를 모두 반영해줬다.
이제 Time Fixed effect를 넣어줌으로써 Time-varying Confounder도 고려해보자 (아래 그림 중 하단 참고)
시간도 고려함으로써 그룹 간 차이도 볼 수 있는 것이다

Q5만 남았다. 읽어보면, Customer 1이 Customer 2와 다르게 treatment 받은 시점이 3일째라면 어떻게 될까?를 고민해보는 문제다
→ 이걸 Staggered treatment라고 한다. Treatment Effect 추정이 살짝 이상하게 뒤틀린다. 이건 나중에 얘기해봅시다
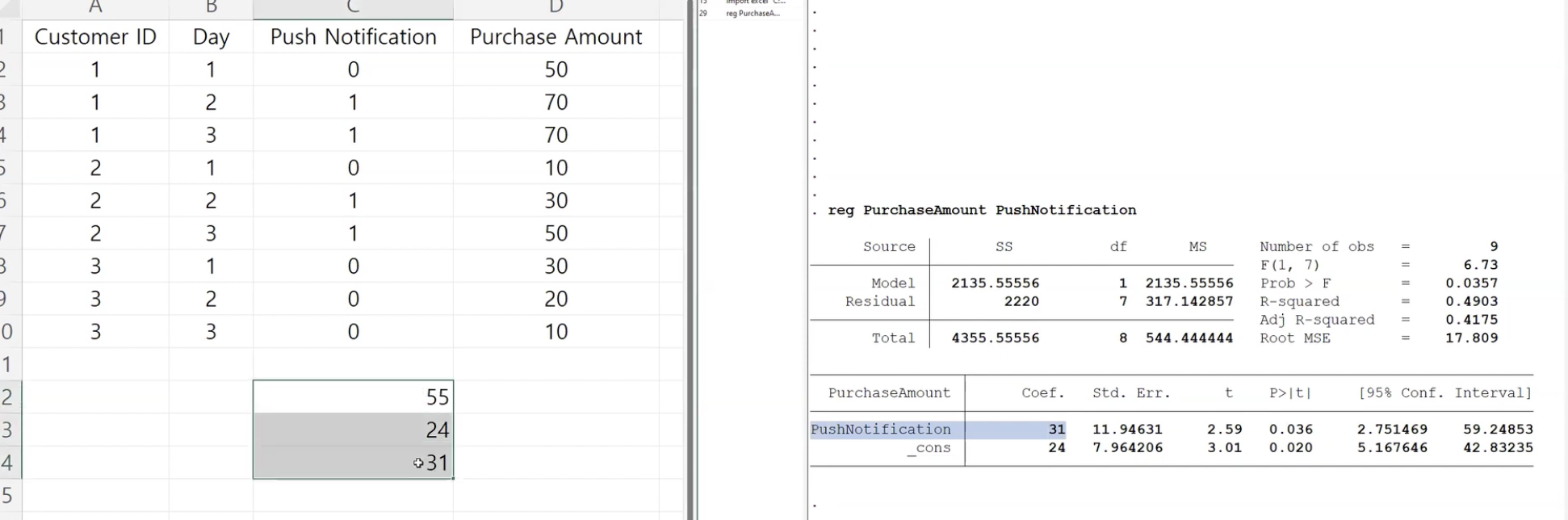
이걸 STATA로 직접 계산해봅시다
Q1: Covariate이나 Fixed Effect가 없을 때는 Treatment와 Untreatment 그룹의 평균 차이를 계산한다.
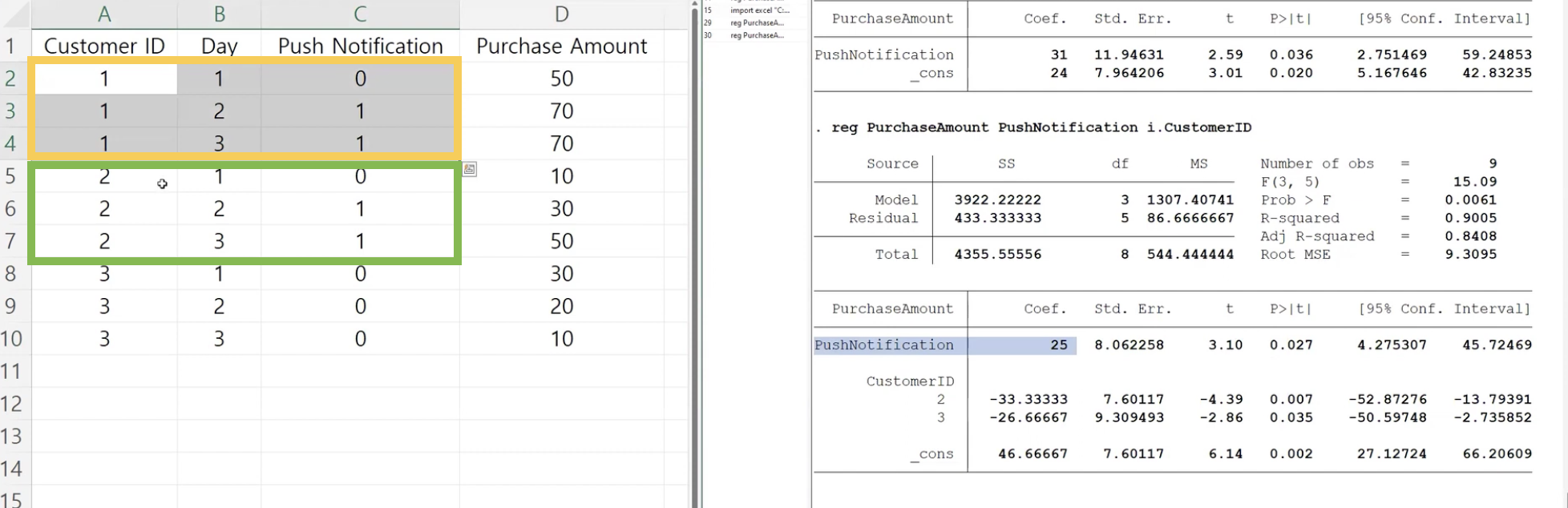
Q2 & Q3: Unit Fixed Effect를 보는 과정이다. Q3은 Control Group을 제외하고 분석하라는 명령어를 추가했다. 그래도 값이 동일함을 볼 수 있죠?
With-in Group(Customer Group) Comparison 하므로 Customer 3에 대한 Fixed Effect 값은 바뀔 수 있어도 25라는 Treatment Effect 계수는 바뀌지 않음
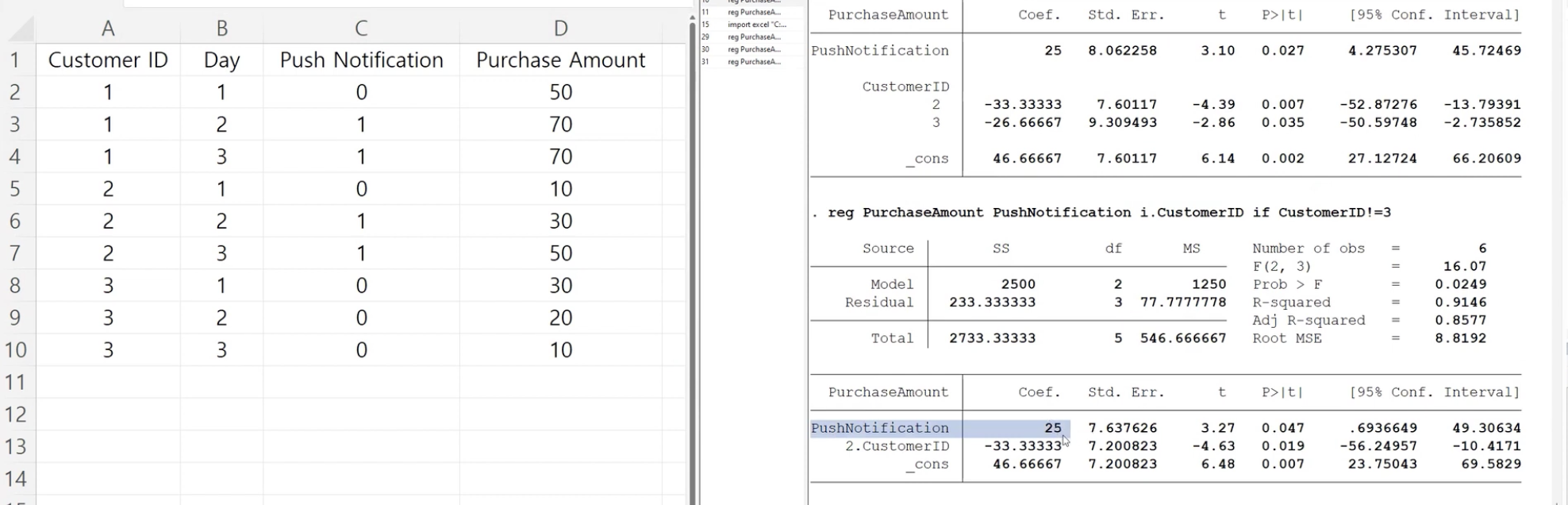
Q4: 이제는 Control Group과 비교하는 Time Fixed Effect을 추가해보자.
값이 크게 바뀜을 확인할 수 있음
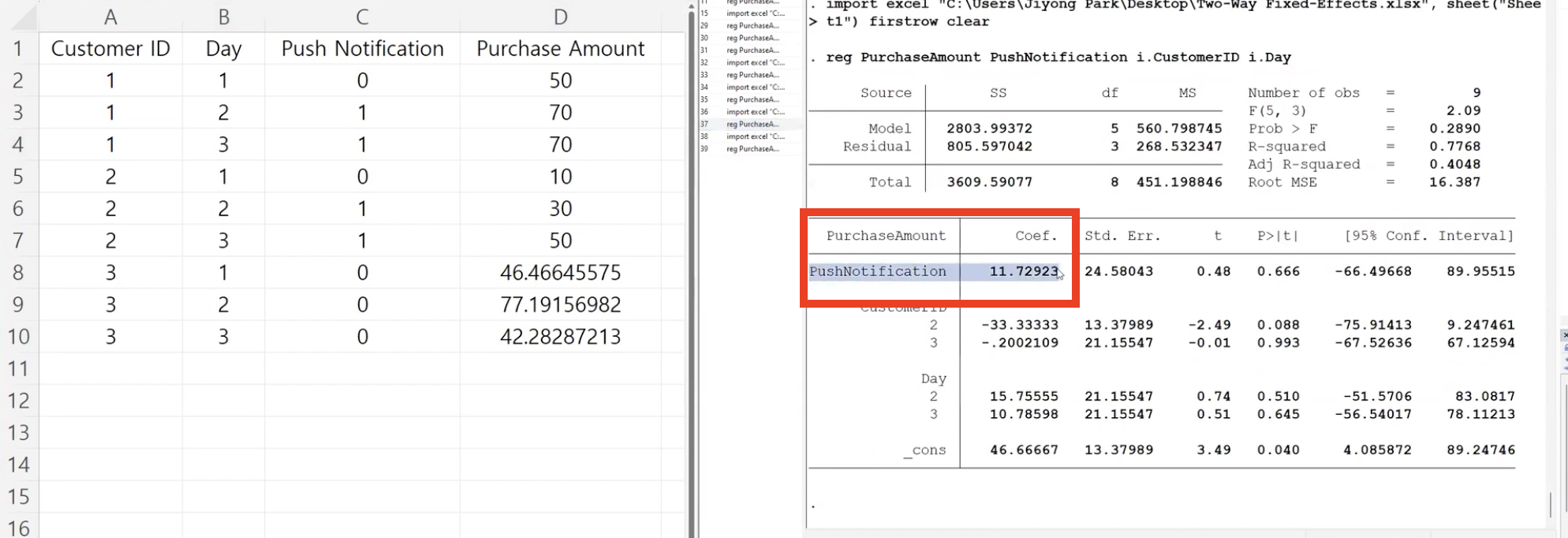
즉, 효과적인 인과추론을 위해서는 Unit 뿐만 아니라 Time Fixed Effect를 추가하는 것이 중요하다!
예) Dale and Krueger (2002) - 사립 대학 프리미엄 연구 사례
비싼 등록금을 내고 사립 대학을 가는게 수입에 영향을 미칠까? 인과관계 파악이 매우 어려움
- 비싼 사립 대학에 다니는 학생과 공립 대학 학생은 대학 말고도 다른 특성에서 차이가 많이 날 수 있어서, 비교가 불가능하다.
- 여러 사회경제적 상황 뿐만 아니라 눈에 보이지 않는 잠재력, motivation, ambition 등등
그래서 이 연구는 같은 대학에 지원하고 같은 대학에서 합격 통보를 받은 학생들을 비교한다.
- 입학사정관이 학생들의 학업정석, motivation 등 종합적으로 고려하고 있을 것이다 → 비교 가능하다고 가정
- 두 학생이 UPenn과 Penn State 둘 다에 합격했다고 생각해보자. 잠재력, 학업수준 등등 여러 특성이 비슷비슷할 것이다.
- 한 명은 사립, 한 명은 공립에 갔는데 졸업후에 연봉이 달라졌다고 한다면? 사립 대학의 인과적 효과에 가깝다고 추론할 수 있을 것이다.
- 문제는 전략은 좋지만 어떻게 구현하고, 데이터를 추정할 것인가?
- 사립 대학과 공립 대학의 연봉 차이를 단순 계산하자면? (아까 Q1에 해당)
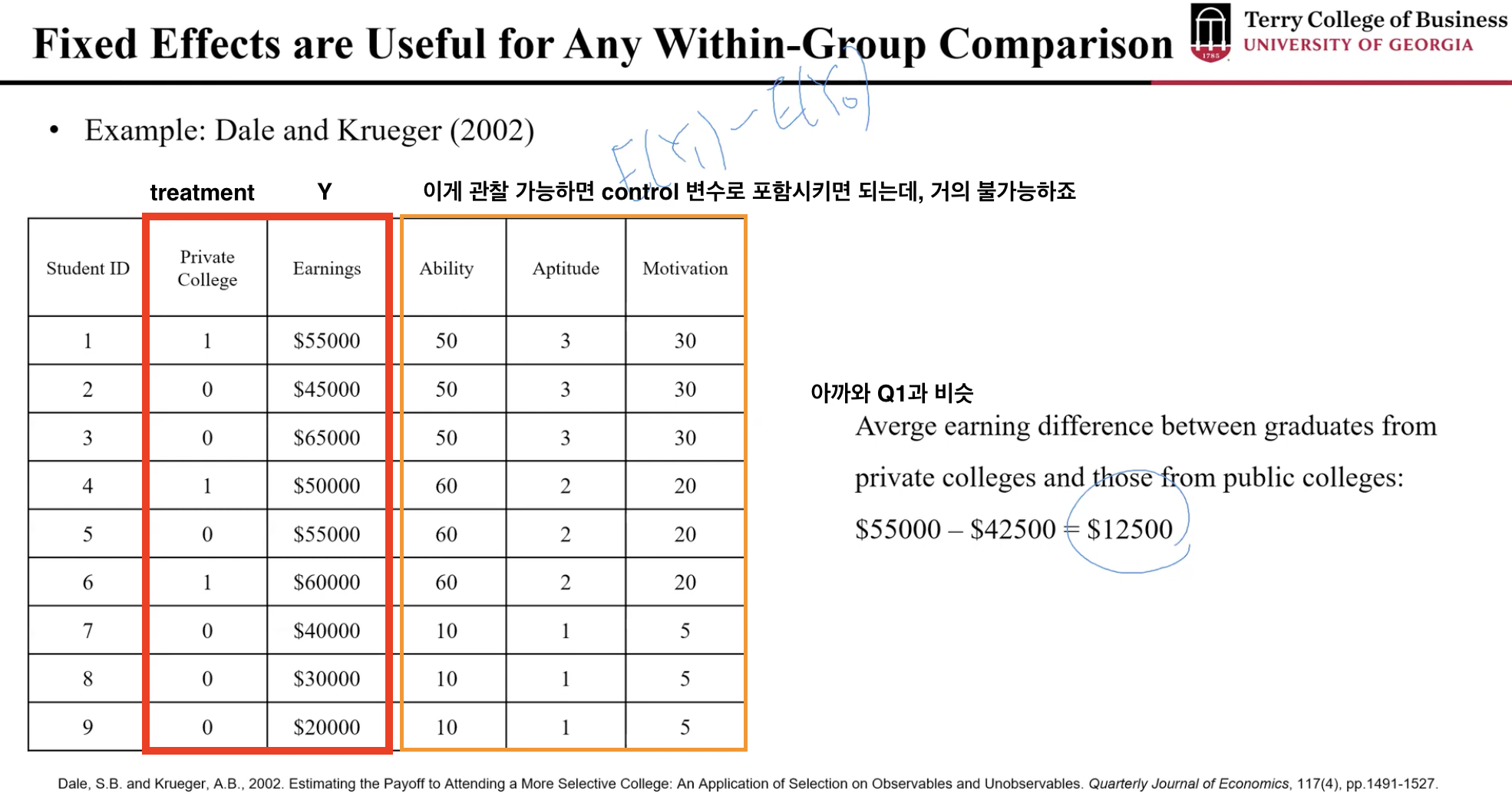
- 이 학생들의 관찰가능한 (하지만 대부분은 관찰 불가능한) 특성들을 제어해주면 좋겠죠... 하지만 현실적으로 힘들다는 겁니다
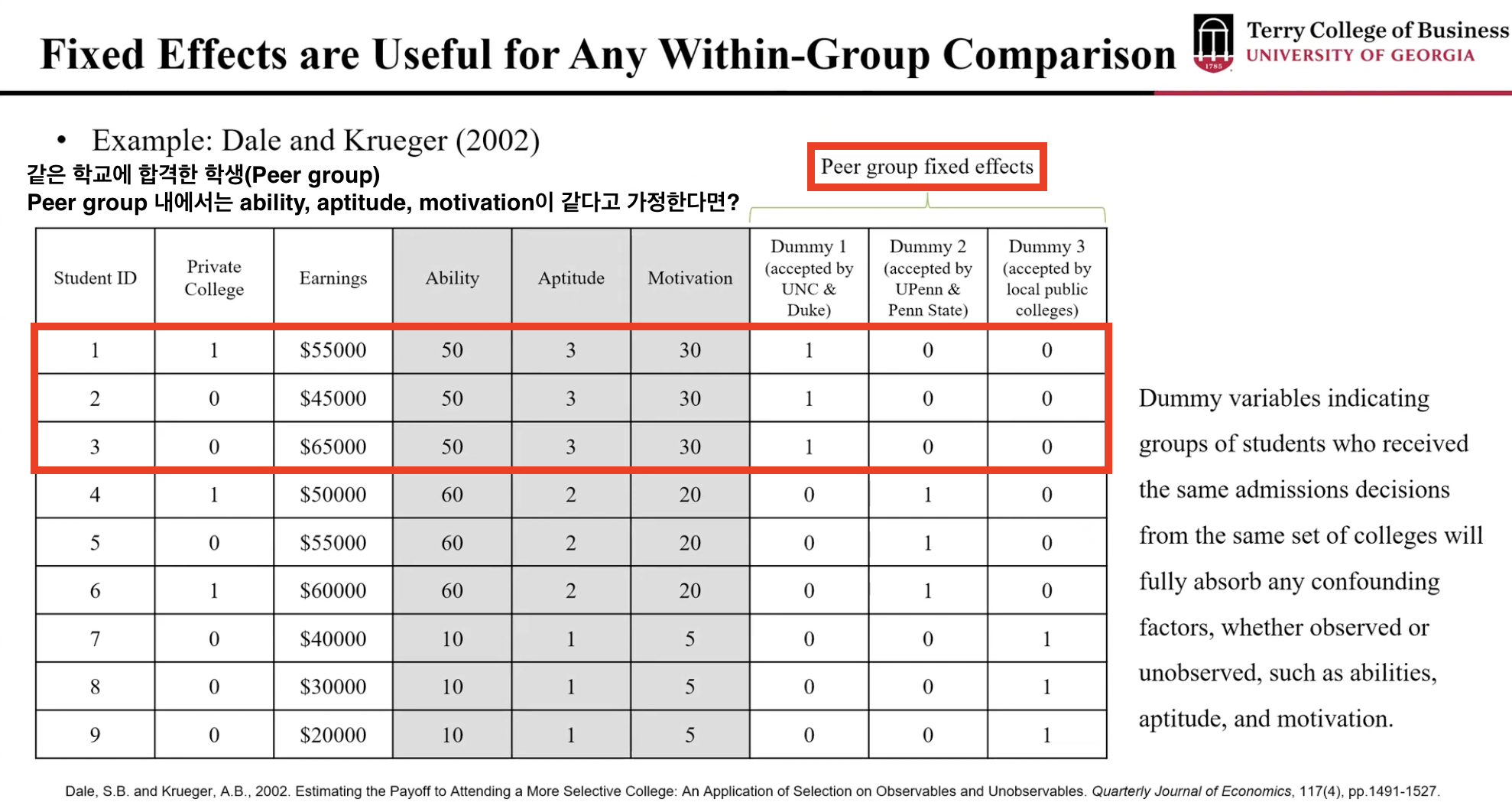
- 그래서 그룹 별로 특성이 비슷하다고 간주하고 Unit Fixed Effect를 넣어주는 것이죠
- 여기서 그룹이라 한다면, UNC랑 Duke 합격 or UPenn이랑 Penn State 합격 이런 식으로...
- 적어도 해당 그룹 내에서는 서로 다른 특성은 사라질거고, 사립대학에 갔냐 안갔냐의 차이만 남게 되니까
→ 즉, Fixed Effect가 With-in group comparison이 가능해진다!
'Data Science > Econometrics' 카테고리의 다른 글
| [Econometrics, 계량경제학] 데이터 구조와 고정 효과(Fixed Effect) (0) | 2024.10.28 |
|---|---|
| [Econometrics, 계량경제학] OLS와 BLUE (1) | 2023.11.21 |
| [Econometrics, 계량경제학] RDD(불연속 회귀 설계) (0) | 2023.09.17 |
| [Econometrics, 계량경제학] 편향(bias) (0) | 2023.09.17 |
