ML 0. 통계분석 | 통계적 추론과 통계적 검정
통계분석(Statistical Analsis)
1. 통계학과 기술통계
2. 확률분포
3. 통계적 추론과 통계적 검정 ← 오늘은 여기!
1번과 2번을 먼저 보고싶다면?
https://heesleisure.tistory.com/28
ML 0. 통계분석
통계분석(Statistical Analsis) 1. 통계학과 기술통계 2. 확률분포 3. 통계적 추론과 통계적 검정 1. 기술통계 데이터의 속성을 특정한 통계량을사용해 정리, 요약, 설명하는 방법 중심척도 중심경향성:
heesleisure.tistory.com
3. 통계적 추론과 통계적 검정
1) 기술통계와 추론통계
- 기술통계: 측정이나 실험을 통해 수집한 통계 자료의 정리/표현/요약/해석을 통하여 자료의 특성을 규명하는 방법과 기법
- 추론통계: 한 모집단에서 추출한 표본에 대해 결론을 추론하는 절차와 기법
*자료수집과 자료정리/요약은 기술통계 영역, 자료가 표본이냐 모집단이냐에 따라 추론통계를 진행

2) 추론통계
|
1) 활용용도
- 통계적 추정: 표본의 성격을 나타내는 통계량을 기초로 하여 모수를 추정하는 통계적 분석 방법
- 가설 검정: 모수에 대하여 특정한 가설을 세워놓고, 표본을 선택하여 통계량을 계산한 다음 이를 기초로 모수에 대한 가설의 진위를 판단하는 방법
2) 이론
- 모수: 모집단(populatoin)의 기술적 척도
- 통계량: 표본(sample)의 기술적 척도
표본으로 구해지는 결론과 추정치는 항상 옳은 것은 아니다.
그래서 통계적 추론에는 신뢰의 척도, 즉 신뢰수준(1-α)과 유의수준(α)이 필요함
3) 추정
(1) 점 추정: 추정하고자 하는 모수를 표본 데이터를 이용하여 하나의 수치로 추정함
(2) 구간 추정: 모수가 존재할 것으로 예상되는 구간을 정하여 추정
- 신뢰수준: 추정하고자 하는 모평균이 구간(신뢰구간)에 포함될 확률
ex) 95% 신뢰수준
3-1) 구간추정
추정하고자 하는 모수가 존재하리라 예상되는 구간을 정함.
모수가 존재하리라고 생각되는 신뢰구간과 그 가능성을 나타내는 신뢰수준(신뢰도)이 필요함
- 신뢰구간: 점추정값 ± 한계 오차
3-2) 신뢰구간의 추정
| 신뢰구간 측정대상 모수 | 사용하는 분포 | 주의 사항 |
| 모평균 | 모표준편차를 알 때: 정규분포 | 모집단이 정규분포일 경우 항상 성립 |
| 모표준편차 모를 때: t분포 | 모집단이 정규분포가 아닐 경우, 표본의 크기만 크다면 중심극한정리에 의해 성립함 |
|
| 모분산 | 카이제곱 | 모집단이 정규분포일 경우 항상 성립 |
| 모비율 |
※ 표준편차와 표준오차의 차이는?
표준편차란, 모집단에서의 퍼짐을 재는 척도
표준오차란, 통계량의 표준편차를 추정할 때 이를 (통계량의) 표준오차라 부름
4) 정규성 검정(Normality Test)
회귀분석 등에서는 확률분포가 정규분포를 따르는지 아닌지 확인하는 것이 중요하다
이러한 검정을 정규성 검정이라고 함
|
[Scipy에서 제공하는 정규성 검정 명령어]
- Shapiro-Wilk test: scipy.stats.shapiro
p-value란, H0(귀무가설)을 지지해주는 확률값.
ex) p-value가 유의수준(0.05)보다 작다면, 영가설 기각(영가설이 사실이라는 확률이 5% 미만이므로
영가설이 사실이 아닐 확률이 95%를 넘으며 이는 신뢰수준에 들어감)
대립가설(내가 주장하는 바) 채택
4-1) 모평균 추정
(1) 모표준편차(σ)를 아는 경우: 정규분포
모평균(µ)에 대한 100(1-α)% 신뢰구간
※ 유의수준에 따른 z 통계값
| 양방향 기준 a | 90% | 95% | 99% |
| z score | ± 1.645 | ± 1.96 | ± 2.58 |
| 단방향 검정 | 0.05(95%) | 0.025 | 0.005 |
| 양방향 검정 | 0.1 | 0.05 | 0.01 |
[양방향 검정]
x upper bar(x의 평균) ± Zα(유의수준에 따른 z값)*σ(모표준편차)/√n
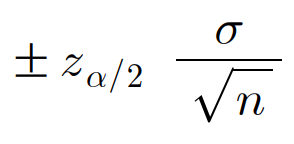
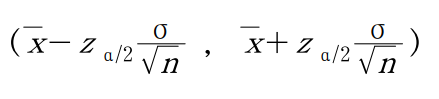
ex) 배추 40개를 랜덤 추출하여 무게를 측정한 결과, 모표준편차는 0.397로 나타남. 이 자료로부터 무게에 대한 95% 신뢰구간을 추정하시오.
#df를 직접 입력
df = pd.DataFrame({"sample": [3.6, 2.9, 2.8, 2.6, 3.4, ... 2.2]})
df.head
#정규분포 구간 추정 함수
lower, upper = stats.norm.interval(0.95, loc=np.mean(df), scale=0.397/np.sqrt(40))
print("신뢰구간: ({0}, {1})".format(lower.round(2), upper.round(2)))
(2) 모표준편차(σ)를 모르는 경우: t 분포
모평균(µ)에 대한 100(1-α)% 신뢰구간
일반적으로 표본으로부터 표준편차를 추정해나가야 함
[미지의 모표준편차(σ) 대신 표본표준편차(s)를 사용]
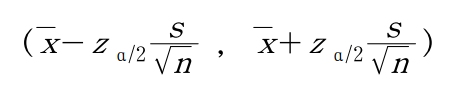
ex) 제품개발자는 새로 개발된 강종의 평균 인장강도가 55kg/㎟으로 기대하고 있음. 20개의 샘플을 랜덤 추출하여 표본평균 54.860, 표본표준편차 1.0081임을 구함. 이 모평균값의 95% 신뢰구간을 추정하시오.
#df를 직접 입력
df = pd.DataFrame({"sample": [54.1, 53.3, 56.1, 55.7, 54.0, ... 55.0]})
#정규분포 구간 추정 함수
lower, upper = stats.t.interval(0.95, len(df)-1, loc=np.mean(df), scale=scipy.stats.sem(df))
#모표준편차를 알 때와 달리 자유도를 추가로 입력, scale에는 표본표준편차를 구하는 함수 입력
print("신뢰구간: ({0}, {1})".format(lower.round(2), upper.round(2)))
★ 모표준편차를 아는 경우와 모르는 경우 둘 다 표본표준편차를 사용하며, 표준편차/√n을 쓰느냐, 표준오차/√자유도를 쓰느냐의 차이
5) 통계적 가설검정
(1) 절차
| 가설 수립 | 가설 검정의 수행 | 검정결과의 판단 |
| 가설 검정의 목적 확인 주장하고자 하는 대립가설(H1)과 그 반대의 귀무가설(H0)을 설정 유의수준(α)를 결정함 → 보통 5%, 1% |
적절한 검정통계량 결정(t, F, x2) 데이터로부터 검정통계량을 계산 데이터로부터 p-value를 계산 |
p-value < 유의수준(a)이면 H0 기각 *대립가설(주장하는 가설) 채택 p-value > 유의수준(α)이면 H0 채택 |
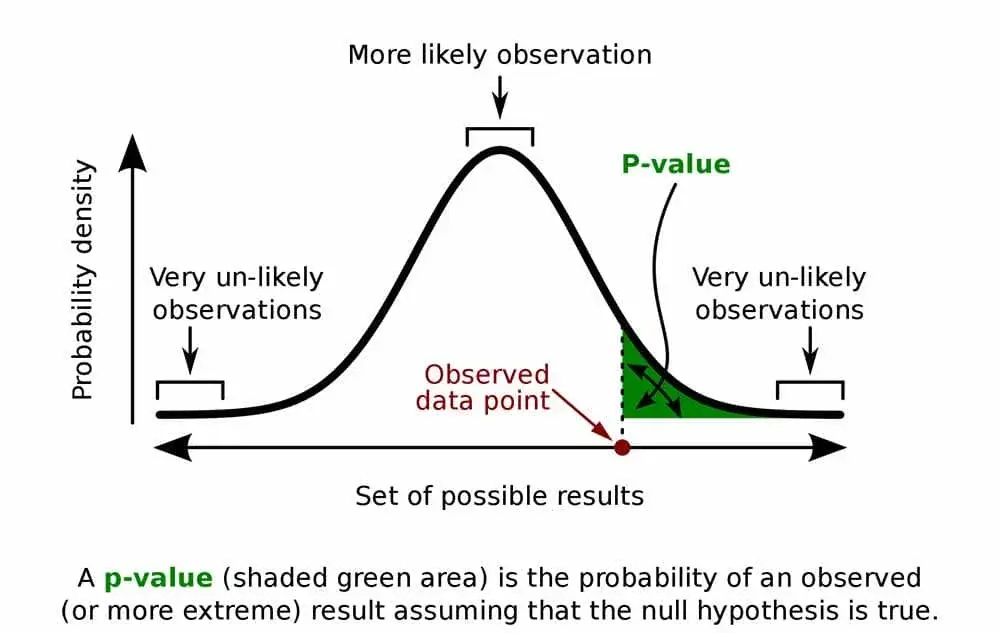
(2) 유의수준과 p-value
- 유의수준(α): 귀무가설을 기각할 때, 그 귀무가설 기각 결정이 잘못될 수 있는 확률(최대가능성)
- p-value: 귀무가설이 참이라는 가정하에, 데이터가 귀무가설을 지지하는 확률
p-value가 유의수준 α보다 작을 때 귀무가설(H0)을 기각하고, 유의수준 α보다 클 때 귀무가설(H0)을 채택함
(3) 가설검정의 오류: 제1종 오류와 제2종 오류

| H0 참 | H1 참 | |
| 귀무가설 H0 채택 | 옳은 결정 (발생확률: 1-α) |
제2종 오류 (범죄를 저질렀는데 무죄, 발생확률: β) |
| 대립가설 H1 채택 | 제1종 오류 (실제 죄가 없는데 유죄판결, 발생확률: α) |
옳은 결정 (발생확률: 1-β) 검정력 |
- 제1종 오류
생산자 위험, 신뢰수준은 1-α
- 제2종 오류
소비자 위험, 귀무가설을 기각하는데 많은 증거를 요구하면 제2종 오류가 일어날 확률이 높아짐
- 검정력: 1-β, 귀무가설이 거짓일 때 이를 기각할 확률(Power of the test)
가설검정과 상관분석 회귀분석은 찢겠습니다...
내용이 너무많아 ~