ML 0. 통계분석
통계분석(Statistical Analsis)
1. 통계학과 기술통계
2. 확률분포
3. 통계적 추론과 통계적 검정
1. 기술통계
데이터의 속성을 특정한 통계량을사용해 정리, 요약, 설명하는 방법
| 중심척도 | 중심경향성: 중심적인 경향을 나타내는 주요한 기술통계 | 산술평균, 중앙값, 최빈치 |
| 산포척도 | 데이터가 퍼져있는 정도를 설명하는 기술통계 | 범위, 분산, 표준편차, 사분위수 범위(IQR) |
| 분포모양 | 데이터가 퍼져있는 형태를 나타낸 것 | 도수분포, 비대칭도(왜도, 치우친 정도), 첨도(뾰족한가 완만한가) |
1) 산포척도
- 범위: 최대값과 최소값의 차이
- 제곱의 합(Sum of Squares)

편차는 다 더하면 0이 되는 딜레마가 생긴다 → MSE(제곱하여 합) / MAE(절대값의 합)
잘 알려진 예는 표준편차, std
① 분산(Variance, Mean Square)
평균에서 각 데이터까지의 거리를 제곱한 수치의 평균. 즉, 각 데이터에서 평균을 뺀 수의 제곱의 합을 하여 데이터 수로 나눔
→ sum of squares를 데이터 수로 나눈 것

이는 표본분산을 구하는 것으로,
n-1을 나누어주는 불편분산을 시행해줌
모분산의 경우 n으로 나눈다.
② 표준편차(Standard Deviation, s)
분산에 제곱근을 하여 구한 값
특이치(outlier, 이상치)에 민감하고 영향을 받음
2) 분포모양
① 도수분포(도수: frequency)
범주형 자료 정리 시 가장 많이 사용됨
도수란, 범주에 속한 관측 개체의 수(=빈도, frequency)
- 상대도수(비율), 누적도수(누적된 데이터 수), 누적상대도수(누적비율)
② 비대칭도(왜도, Skewness)

왜도가 양수일 때 왼쪽으로 치우쳐진 모양
최빈값 > 중앙값 > 평균
왜도가 음수일 때 오른쪽으로 치우쳐진 모양
평균 > 중앙값 > 최빈값
③ 첨도(Kurosis)

분포모양이 얼마나 뾰족한가, 완만한가를 나타내는 정도
첨도가 커질수록 모양이 뾰족해지고
첨도가 작아질수록 모양이 완만해짐
데이터 유형
- 연속형(Continuous) 데이터: 등간척도, 비율척도
- 이산형(Discrete) 데이터(범주형 데이터): 명목척도, 서열척도
| 명목척도 | 서열척도 | 등간척도 | 비율척도 |
| - 대상을 단순히 구분하기 위해 숫자를 부여함 | - 대상의 속성에 크기에 따라 순위, 서열을 부여함 | - 측정된 변수간 가감 연산(+, -) 가능 - 같은 간격을 가지지만 절대영점이 없어 비율관계는 성립하지 않음 - 상대적 차이로만 나타남 |
- 절대영점 존재 - 등간척도 + 비율 개념 - 가감승제와 같은 모든 사칙연산이 가능함 |
| 성별, 품질(양품/불량), 운동선수 백넘버, 주민등록번호 |
만족도(1~5), 학교성적등급, 크기(S,M,L) |
온도, 물가지수 | 중량(kg), 강도 |
| 중심경향치를 나타낼 때, 최빈값 | 중심경향치를 나타낼 때, 중위값 | 중심경향치를 나타낼 때, 산술평균 |
중심경향치를 나타낼 때, 산술평균, 기하평균 |
| 빈도분석, 비모수통계 | 비모수통계 | 모수통계 | |
2. 확률분포
확률
- 확률: 특정 사건이나 결과가 발생할 가능성
- 확률의 조건
1_Random Process
2_Mutually Exclusive outcomes: 동시에 두 사건이 발생할 수 없음
3_Law of Large Numbers: 시행 회수를 많이 할 수록 특정 결과가 발생할 비율은 자체의 가능성에 점점 수렴함
4_ Independence
- 표본공간
실험결과 발생할 수 있는 모든 가능한 결과의 집합
- 확률변수
표본공간상의 모든 가능한 결과에 특정 수치를 부여하는 것
ex) 앞면(H) → 1, 뒷면(T) → 2
1) 확률변수
| 이산확률변수 | 연속확률변수 |
| 확률변수가 취하는 값이 유한개일 때 ex) 동전을 세 번 던지고, 그 결과를 기록하는 실험의 표본공간 S에서 이산확률변수 X = 동전 앞면의 수 |
구간내의 임의의 모든 점을 취할 수 있는 때 ex) 막대기의 길이, 공을 던지는 독립시행에서 던져진 거리, 확률밀도함수 f(x)와 확률 F(X) |
확률분포
- 확률함수
확률변수(x)에 대하여 정의된 실수를 0과 1사이의 실수(확률)에 대응시키는 함수

| 이산확률함수(PMF) | 연속확률함수(PDF) |
 = 확률질량함수 Probability Mass Function |
 = 확률밀도함수 Probability Density Function |
- 누적확률함수(Cumulative Probability Distribution Function, CDF)
확률변수 X가 x 이하의 값을 취할 확률
(F(x) = P(X ≤ x))
- 확률분포
확률변수가 특정 값을 가질 확률, 즉 상대적 가능성
시행횟수가 늘어날수록 정규분포에 가까워짐
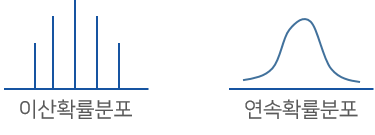
- 확률분포의 종류
확률변수 데이터 유형에 따른 이산확률분포와 연속확률분포
| 연속확률분포 | 정규분포 |
| 표준정규분포 | |
| t 분포 | |
| x^2 분포(카이제곱 분포) | |
| F 분포 | |
| 와이블 분포 |
| 이산확률분포 | 베르누이 분포 |
| 이항 분포 | |
| 포아송 분포 | |
| 초기하 분포 |
- 연속확률분포
① 정규분포(Normal Distribution)
평균을 중심으로 좌우 대칭인 종모양 분포(Gauss 분포)
x의 평균 µ와 그 표준편차 σ인 두 모수에 의해 그 분포의 특징이 결정됨
용도: 수집된 자료의 분포를 근사하는 데 자주 사용됨. 중심극한정리에 의하여 독립적인 확률변수들의 평균은 정규분포에 가까워지는 성질이 있기 때문
* 확률밀도함수 = 연속확률함수(PDF)
| 정규분포의 특징 ・ 평균 = µ(분포위치), 분산 = σ2(분포모양) ・ 종모양이며, µ를 중심으로 대칭 ・ 기호: X ~ N(µ, σ2) |
② 표준정규분포(Standard Normal Distribution)
정규분포 밀도함수를 통해 X를 Z로 정규화함으로써 평균이 0, 표준편차가 1인 표준정규분포로 나타냄
용도: z-분포로 하는 검정(test)을 z-검정(z-test)이라고 한다.
・ 기호: Z ~ N(0, 1)
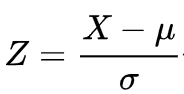
- 확률계산
정규분포를 표준정규분포로 변환하여 표준정규분포표를 이용하여 확률을 계산
③ t-분포
정규분포의 평균을 측정할 때 주로 사용, 정규분포처럼 평균을 중심으로 대칭
표준정규분포보다 평평하고 기다란 꼬리를 가짐(양쪽 꼬리가 두터운 형태)
자유도에 따라 t분포의 모양이 바뀜
용도: 모집단의 평균 추정, 검정
모평균의 추・검정에서 모표준편차를 모를 때 정규분포 대신 사용됨
표본의 크기가 더 적으면 적을수록 분포의 꼬리는 더 평평해짐
④ 카이제곱(Chi-square) 분포
정규분포를 따르는 모집단에서 크기가 N개인 표본을 무작위로 반복하여 추출하였을 때,
각 표본에 대해 구한 표본분산들은 카이제곱 분포를 따름
(N개의 표본들을 단순히 더하지 않고 제곱을 하여 더하면 양수만을 가지는 분포가 된다. 이것이 카이제곱분포)
용도: 모집단의 분산 추정, 빈도 기반의 분포 또는 형태 적합도 검정(범주형 자료의 적합도 검정), 여러 집단 간의 독립성/동질성
0이 없음. 분산으로 그려서.
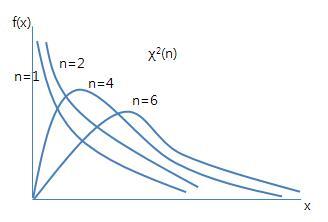
자유도가 커질수록 정규분포모양이랑 비슷해짐
| t-분포 | 카이제곱(Chi-square) 분포 |
| 모집단의 평균 추정 | 모집단의 분산 추정 |
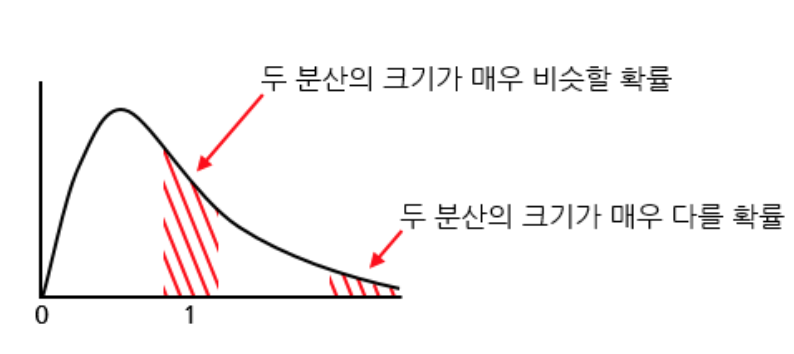
⑤ F분포
두 모집단의 분산에 대한 비의 추정으로, 분산분석과 회귀분석의 통계적 추론에서 기준이 되는 표본분포
집단수-1과 표본수-1이라는 두 개의 자유도 n1, n2에 의해 분포 모양이 결정된다.
카이스퀘어 분포와 마찬가지로, 분산을 다룰 때 사용하는 분포이며 종형의 대칭 분포가 아니다.
카이스퀘어 분포가 한 집단의 분산을 다뤘다면, F분포는 두 집단의 분산을 다룬다.
(자유도에 따라 형태가 달라지며, n1과 n2가 클수록 정규분포에 근사한 형태)
0보다 큰 영역에서만 그려진다.
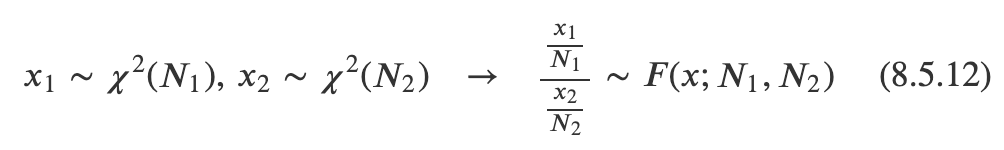
https://math100.tistory.com/46
참고
F분포란?
F분포는 카이제곱분포와 마찬가지로 “분산”을 다룰 때 사용하는 분포인데, 카이제곱분포가 한 집단의 분산을 다뤘다면, F분포는 두 집단의 분산을 다룬다. 그리고 두 집단의 분산이 크기가 서
math100.tistory.com
- 이산확률분포
① 이항분포
베르누이 실험을 여러 번 시행해서 특정한 횟수의 성공/실패 또는 양품/불량품이 나타날 확률을 알고자할 때, 사용되는 분포
*베르누이 분포의 경우 시행횟수가 n=1인 이항분포(특수한 경우)
일반적으로 확률(p)가 0.5이고 시행횟수가 무한대일때 이항분포는 정규분포에 가까워짐
1) 확률밀도함수 P(X=x) - nCx * p^x * (1-p)^(n-x)
2) 기대값 E(x) = np
3) 분산 V(X) = np(1-p)

- 표본의 평균 분포
✔️ 중심극한정리 (★★★)
평균이 µ이고 분산이 σ^2인 임의의 확률분포를 따르는 모집단으로부터 크기 n인 확률표본을 취했을 때,
이 확률표본의 표본평균의 분포는 표본의 크기 n이 충분히 클 때 대략 정규분포를 따름
(표준오차: σ/√ n)
| 1) 모집단이 정규분포이면 표본평균은 표본크기에 상관없이 언제나 정규분포임 2) 모집단이 적어도 대칭형이면, 표본 크기는 5~20이면 표본평균은 정규분포에 가까워짐 3) 모집단이 정규분포에서 얼마나 벗어났느냐와 상관없이 표본크기가 30이상일경우 표본평균은 정규분포에 가까워짐 |
통계적 추론은 다음 글에~
